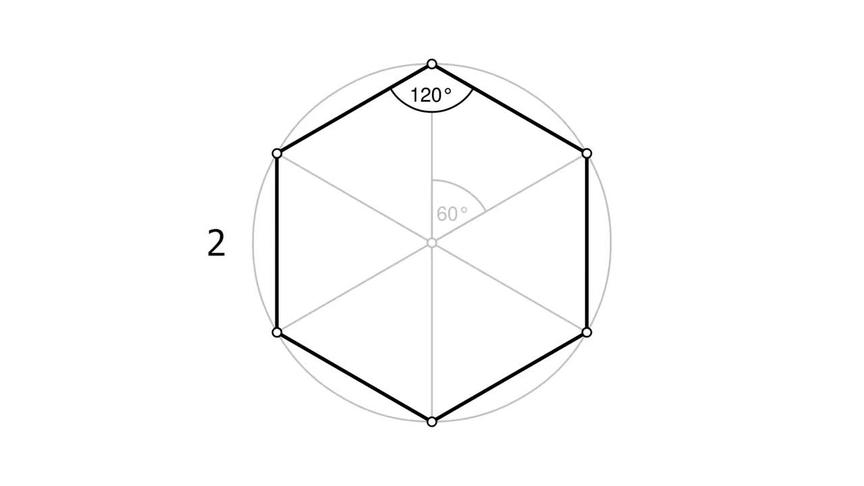
正多角形の内接円 夏休みの宿題でわからなかったのでひらいた。 あまり参考にならなかったです。 ↓^д^; この調子で、正六角形 \((p=6)\) で構成する場合も考えてみましょう、 正六角形の内角は1°です。 「1つの頂点に集まる面の数は3以上」なので \(q=3\) から考えますが これだと、「1つの頂点に集まる角の和が360°未満」という条件を満たしていません。 ぴったり360°だと、立体を構成★n 角形の内角の和= 180 (n 2) ★n 角形の外角の和= 360 正六角形の内角の和は;
正六角形面积计算器 计算专家
正六角形内角
正六角形内角-正六角形(せいろっかくけい)とは、各辺の長さがすべて等しく、内角も1゚と一定な六角形である。一辺をaとすれば周長は であり、外接円の直径(対角長)は であり、内接円の直径(対辺の距離)は であり、面積は下記のとおりとなる。 ・正六角形 正六角形 とは、6つ全ての辺の長さが同じで、6つの頂点の 内角 が1°である六角形です。 下の図は、 正六角形 の例です。



悟空问答 五边形内角和是多少 个回答
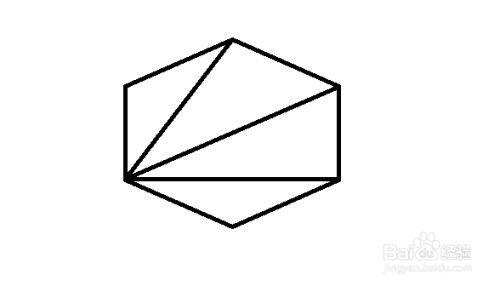
内角の和 180° 18=9 正六角形 頂点 6 点 辺 6辺 内角 1° 内角の和 7° 7=9 正九角形 頂点 9点 辺 9辺 内角 140° 内角の和 1260° 1260=9 対角線の本数 27 27=9 3,6,9の繋がりは正三角形、正六角形、正九角形にも現れています。 ここまで3,6,9が出てくると気持ちいいですね。 日常に潜む3 6 9 日常に潜む 正四角形(正方形)は対角線で三角形2個に分けられるので 正方形の内角の和は180°×2=360° 同じように考えて 正五角形は三角形3個分で180°×3=540° 正六角形は三角形4個分で180°×4=720° 各角の大きさは 正五角形は540°÷5=108° 正六角形は720°÷6=120° 「一辺の角度は何℃か」はわかりませんでした。 36人 がナイス!三角形の数で内角の和が計算できます 五角形と六角形の内部に作成できる「三角形の数」「内角の和」は下の図の通り。 四角形と同じように、三角形の数が分かれば内角の和は求められますよね^^ どうですか? ここまではそれほど難しくないと思います。 多角形と言っても、まだまだ五角形、六角形と数が少ない形ですからね。 ということで! ここで一気に
四角形の内角の和: 360° 360 ° 五角形の内角の和: 540° 540 ° 六角形の内角の和: 7° 7 ° ・・・ n角形の内角の和: 180°× (n−2) 180 ° × ( n − 2 ) この公式は覚えやすいので暗記してもいいのですが、簡単に導出できるため、わざわざ覚える必要もありません。 ではどのようにこの公式を導出するのか、なぜ内角の和が「 180°× (n −2) 180 ° × ( n円に内接する正多角形 後から星形をカッターで切り抜いた。 大きさは色々でも、形が揃う為。 円を近似するのに何角形くらいで十分か確認するために使用しました。 ありがとうございます! じゃがいもの面取りで効率が良いのは7面というお話があり、数値を出すために使いました。 じゃがいもを円柱と見立てた場合の廃棄率は、6面1730%、7面1290%、8面997正六角形(せいろっかくけい)とは、各辺の長さがすべて等しく、内角も1゚と一定な六角形である。 一辺をaとすれば 周長 は 6 a {\displaystyle 6a\,\!} であり、外接円の直径(対角長)は 2 a {\displaystyle 2a\,\!}
正多角形(せいたかっけい、せいたかくけい、regular polygon)とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。 また、正偶数角形は点対称の図形でもある。 辺の数が同じ正多角形どうしは全て互いに180 (6 2) = 7 ⇒ 1 つの内角は7 6 = 1 正六角形の外角の和は;・平行線と角,三角形の内角,多角形の内角と外角に関する内容は,推論のもとにな る基本の性質としてその知識をまとめることが大切である。同時に,これらの性質 の関連をいろいろと考えさせることは,論理的に推論することを深める点で重要で ある。 ・また,平行線や多角形の角に関�




正六边形面积公式及特征怎么判定轴对称图形 公式大全 正六边形的判定 Duboot网




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ
正三角形~正六角形あたりまでは出題されやすいため、覚えておくと便利です。 ちなみに、正七角形の一つの内角は$$\frac{180°×5}{7}=\frac{900°}{7}=°$$ となり、整数値にならないためほぼ出題されることはないでしょう。 ※正八角形の一つの内角・外角は整数値になるため、ふつうに 先生:正三角形の1つ分の角の大きさは? 児童:60度 先生:どうやって求めたの? 児童:180÷3 先生:3はどういう意味? 児童:三角形の3 次に、正六角形の内角の大きさの求め方も確認します。内角の和ではなく、正六角形の1つの内角の大きさは1度とでも、ありがとうございました! ^ω^ 面倒な計算をしなくて済んだので非常に助かりました。 ありがとうございました。 アンケートにご協力



正六角形面积计算器 计算专家




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
角形の内角の和は180(n2) 度であることを説明し,そ のことから正多角形の内角の大きさが求められること を,正六角形を例に挙げて説明した。この説明は講義形 式で行い,その後,正五角形や正七角形の内角の大きさ を演習問題として出題した。 問題2 ①正五角形の内角の和と,一つの内角正6角形の一つの内角の大きさは何度だろう。 クマ 図で書いた青い角度が内角だね。 タヌキ 6角形の内角の和は、180×4=7°だね。 スコア★0★ 次へ進む(内角) (外角) =180° (外角) =180°− (内角)




六边形 维基百科 自由的百科全书



六角形的内角和怎么算 六边的内角和怎么算 怎么算
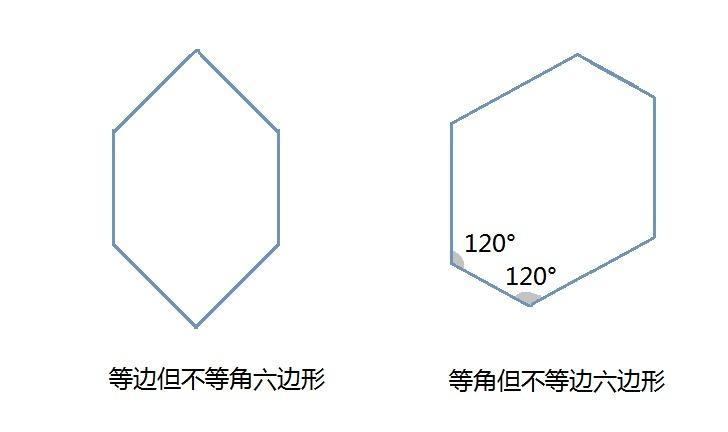
四角形の内角の和を考える。 12 多角形の内角の和を調べる。 なるほど,すごいすごい。それで,正五角形も同じように計算できるんだ。それなら正六角形はどうなるんだろうね。まず六角形の角の和は求められる。 c21 六角形は三角形4つに分けられるので7°になります。(黒板に図正六角形 A 正六角形六角 六角形は、等しい辺で構成されています。長さですが、頂点は2つの異なる内角を交互にしています。 これらの2つの形式は、互いにデュアルであり、正六角形の半分の対称次数を持っています。 i4 フォームは、1つの対称方向に沿って平らまたは引き伸ばされた正⑴ 正五角形 ⑵ 正六角形 ⑶ 正八角形 内角の和〔〕 内角の和〔〕 内角の和〔〕 外角の和〔〕 外角の和〔〕 外角の和〔〕 1つの内角〔〕 1つの内角〔〕 1つの内角〔〕 1つの外角〔〕 1つの外角〔〕 1つの外角〔〕 p90 1 チェック1 x 70ß 45ß x 55ß 130ß x 40ß 145ß p90 2



コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫




六边形 维基百科 自由的百科全书
N 0 gb Æ0 b ô Óu ' 180 r >& > >0>'_>E >& > >0>'b á #0 A _M >& > >0>'b á #0 M G\ _1"8 @6~>* 8l!lb X Æ 0 b X 4E ¥KS#Õ b m正六角形(正6角形)の内角の和は、 180°×(n-2) =180°×(6-2) =180°×4=7° 内角の和、外角の求め方は下記が参考になります。内角1つ分の大きさは $$\large{=108°}$$ となります。 同様に 正六角形の1つ分の内角は\(=1°\) 正八角形の1つ分の内角は\(=135°\) 正九角形の1つ分の内角は\(=140°\) 正十角形の1つ分の内角は\(=144°\) 正十二角形の1つ分の内角は\(=150°\)




正六边形 搜狗百科



生活中的数学之奇妙的蜂窝构造 腾讯新闻
正方形の1つの内角は90°,正六角形の1つの内角は1゜,正十二角形の1つの内角は150°なので,それぞれ1つずつで合計360°になる。 わたしが作成するオリジナル教材(「 自宅でできる受験対策ショップ ワカルー!外角=外角と隣り合わない内角の和 例えば下図の三角形の外角=3050=80度です。 上式を覚えておけば簡単に外角が算定できます。 なぜ外角=外角と隣り合わない内角の和となるか解説します。 三角形の内角の和は180度です。 角度の大きさをA、B、Cと正六角形(せいろっかくけい)とは、各辺の長さがすべて等しく、内角も1゚と一定な六角形である。 一辺をaとすれば 周長 は 6 a {\displaystyle 6a\,\!} であり、外接円の直径(対角長)は 2 a {\displaystyle 2a\,\!}



六边形 搜狗百科



多角形の内角の和を簡単に求める方法 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ
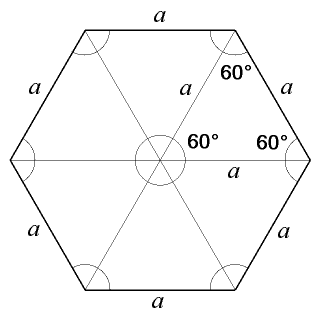
正六角形がイラスト付きでわかる! 全ての辺と角が等しい六角形。 概要 六角形における正多角形。内角は1°。 単独で平面充填が可能な正多角形全3種の内の1種。 中心と各頂点とを結ぶと6つの正三角形が現れる。 これは「中心と頂点との間の距離」と「辺の長さ」とが等しい事を意味し 三角形が4つ、三角形の内角の和は180゚ですから 六角形の内角の和は7゚正六角形なので 内角の大きさは皆同じですからひとつの角は1゚になります。 最初に戻って n角形 で考えます。 4角形では対角線が1本引けて三角形2つに分けられます。 5角形では対角線が2本引けて三角形3つに分けられます。 6角形では対角線が3本引けて三角形4つに分けられます。 7360 ⇒ 1 つの外角は360 6 = 60 よって;



正六角形の合計の角度と一つの角度の求め方を教えてください 公式とかも教 Yahoo 知恵袋



数学中六边形的内角和是多少度 初三网
今日は、早稲田中の今年の入試問題2⃣を解いていきましょう! 21年 早稲田中2⃣(1) 角度 正五角形の一つの内角は、108°(180°×(5ー2)÷5 = 540°÷5 = 108°)思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル 点( )は正六角形の各辺の真ん中の点を表します。色のついた正六角形の面積は正六角形abcdefの面積の何倍ですか。1辺が4cmの正六角形abcdefと 正六角形pqrstuは内角がすべて1度だから 相似です。よって、1辺例えば、upの長さを求めます。 こう考えれば、高校生風に思いつきました。もちろん、中学校入試問題ですから、 小学校の考え方でしょうが、とりあえず、高校の考え方でいきます。




六边形内角和怎么算 百度经验




六边形 Wikiwand




多角形の内角の和 算数の公式覚えてますか



小学生算数正六角形の角度を求める問題 詳しい説明でお願いします Yahoo 知恵袋



1




中2数学 六角形の内角の和が3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



Turtle六边形绘制 Enon式微的博客 Csdn博客 Turtle六边形绘制



正六边形任意两点之间的电阻六边形的每两点之间的连线上放置一个单位电阻 求任意两点之间的电阻 作业 慧海网



正六角形 ゆるゆるプログラミング
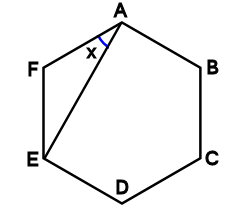



正五角形の中の角度



六边形 Wikiwand




六边形 搜狗百科



南山中学女子部過去問題演習



正六角形面积计算器 计算专家




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




如图 正六边形的每个内角都相等 则其中一个内角a的度数是 快资讯
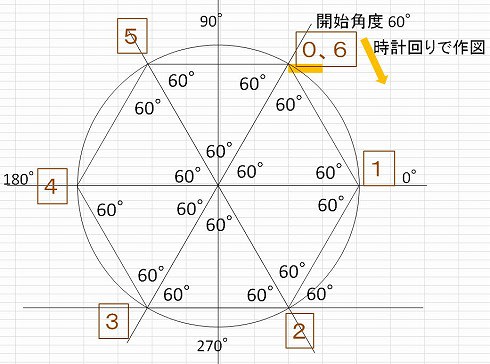



画像をダウンロード6角形角度 シモネタ




计算内角之和 提示 21



正六边形地图 蜂窝拓扑结构在slg地图布局中的应用 It Learner123 Chinaunix博客
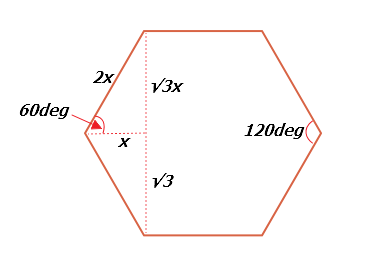



Css画正六边形 Luke Li 博客园




多角形の内角の和 外角の和の公式 数学fun




初三数学 正六边形每个内角的度数是外角的二倍 这个说法正确吗 网易公开课



悟空问答 五边形内角和是多少 个回答



中考数学 不规则六边形每个内角都是1度 求六边形周长 哔哩哔哩 つロ干杯 Bilibili




六边形 Wikiwand




正多角形の内角と外角の大きさ 具体例で学ぶ数学



六边形的内角 西瓜视频搜索




新しい六角形内角 壁紙配布



六角形内角切割视频 西瓜视频




中学生の数学 正六角形の内角 外角 画像 手書きで申し訳ありません Okwave



正六边形 晓茵万事通



六边形的内角和是多少度 初三网



多边形内角和公式 山香教师资格考试总部 品牌新闻



六边形内角和怎么算 百度经验




五边形内角和 五边形内角和是多少度




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト




中学生の数学 正六角形の内角 外角 画像 手書きで申し訳ありませ 数学 教えて Goo




三角形六角形点内角png图片素材免费下载 图片编号 Png素材网



六边形的内角 西瓜视频搜索




六边形网格 探索者专栏 Csdn博客 六边形网格



六边形内角和怎么算 百度经验



关于六边形地图的一些理论与思考 六边形一个的内角和 Duboot网




三角形正六边形




新しい六角形内角 壁紙配布




多边形六角形字典平移 六边形png图片素材免费下载 图片编号 Png素材网



梯形内角分别是多少度 正六边形内角多少度 正六边形怎么画



六边形的内角 西瓜视频搜索



证明 六边形内角和7 三种方法教会大家 哔哩哔哩 つロ干杯 Bilibili



六边形的内角和是多少怎么计算 初三网




七角内角正多边形六角形png图片素材免费下载 图片编号 Png素材网




中学生の数学 正六角形の内角 外角 画像 手書きで申し訳ありませ 数学 教えて Goo



六边形的内角 西瓜视频搜索



Q Tbn And9gctvhdzpuoiri Qxewazwihxzd3b3utfh7tvoa8ss5w Usqp Cau




正六边形内角 正六边形的内角和是多少度 每一个内角为多少度 三人行教育网 Www 3rxing Org




八角形正多边形内角六边形不规则线png图片素材免费下载 图片编号 Png素材网




正六边形内角多少度第1页 驾考预约大全




六边形 维基百科 自由的百科全书



正六边形内角多少度 六边形的内角和是多少度 双偶网




七年级数学检测 Doc 文档分享网



多边形的内角和与外角和 Ppt课件 第一ppt



正6边形内角度数 西瓜视频搜索



六边形 快懂百科




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



6つの内角が等しい六角形は正六角形である 答え 正しくない とあるのです Yahoo 知恵袋



悟空问答 五边形内角和是多少 个回答




六边形 维基百科 自由的百科全书
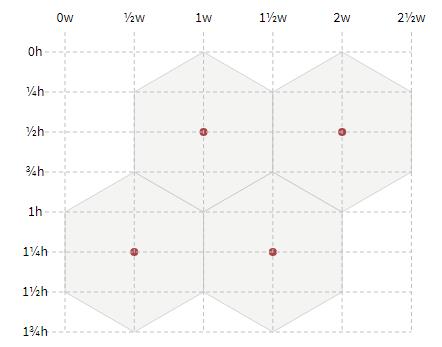



正六边形网格化 Hexagonal Grids 原理与实现 Dhutobuaa 博客园



为什么瓷砖可用三角形 正方形 正六边形平铺而别正多边形不行 新闻 蛋蛋赞
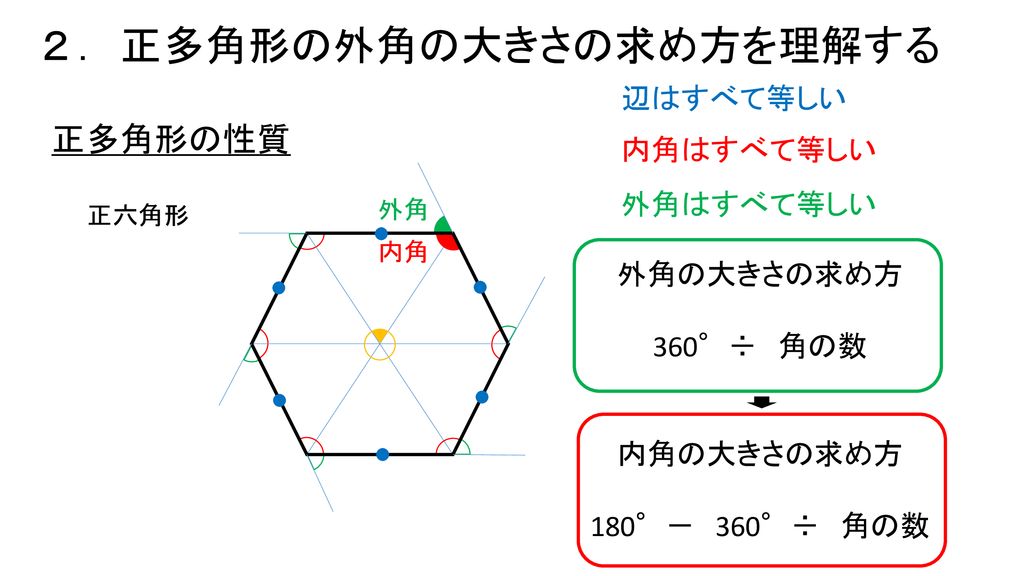



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download



六边形的每个角是多少度 搜狗搜索



如图 正六边形的每一个内角都相等 则其中一个内角a的度数是




六边形内角和是多少度正六边形内角多少度 六边形内角和怎么算



江苏省竞赛 六边形每个内角都是1度 求六边形周长 网易视频




正六边形内角多少度第1页 驾考预约大全




多边形的内角



1



正六边形的内角和是多少度 初三网



六边形 维基百科 自由的百科全书
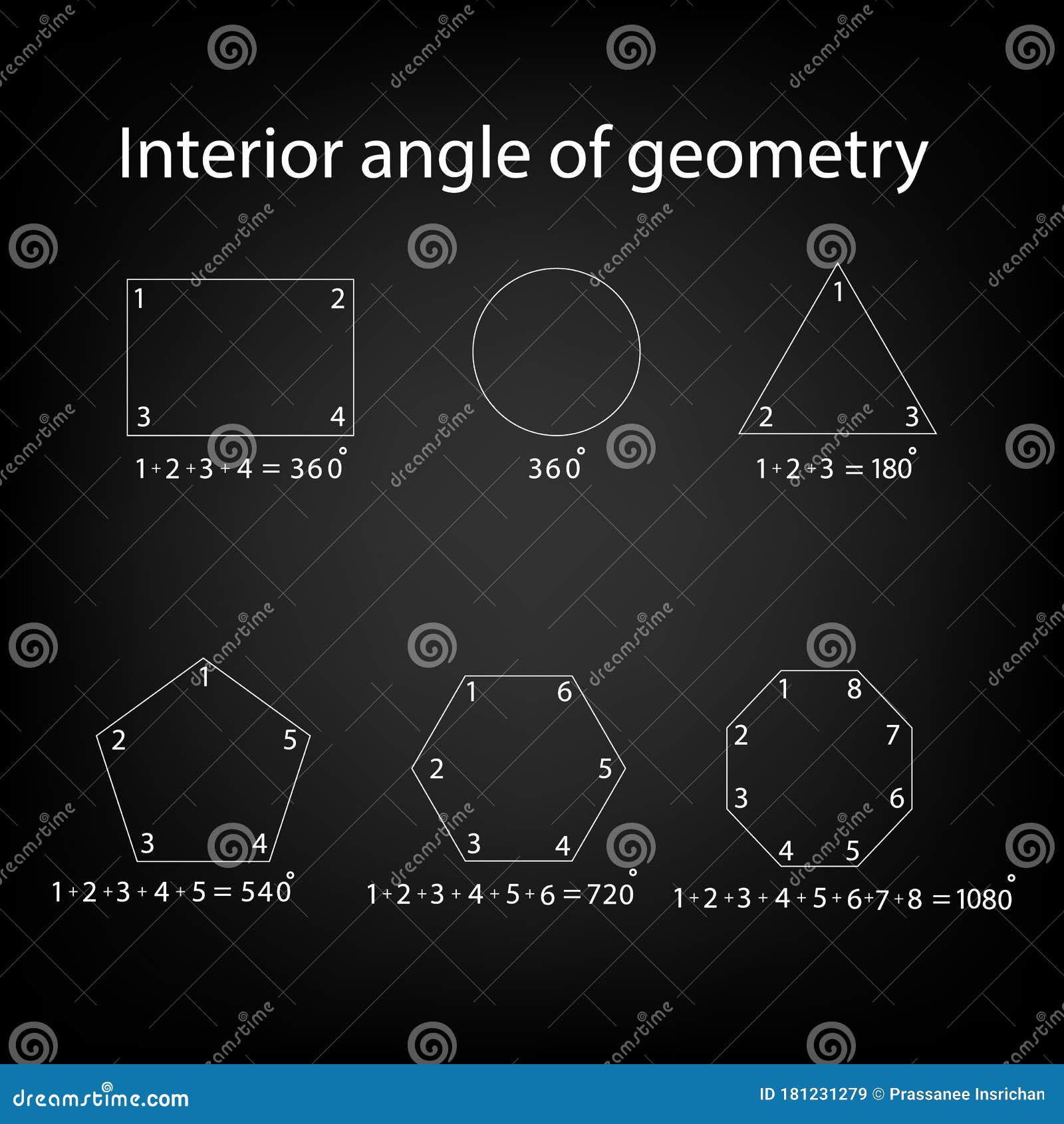



黑色背景上矩形 三角形 圆 五角形 六边形和八边形等几何的内角等式向量例证 插画包括有配方 线路



等边六边形 万图壁纸网




多角形の内角の和 算数の公式覚えてますか



六边形简单 万图壁纸网




正六边形内角多少度第1页 驾考预约大全




正六边形内角 正六边形的内角和是多少度 每一个内角为多少度 三人行教育网 Www 3rxing Org




正六边形 搜狗百科
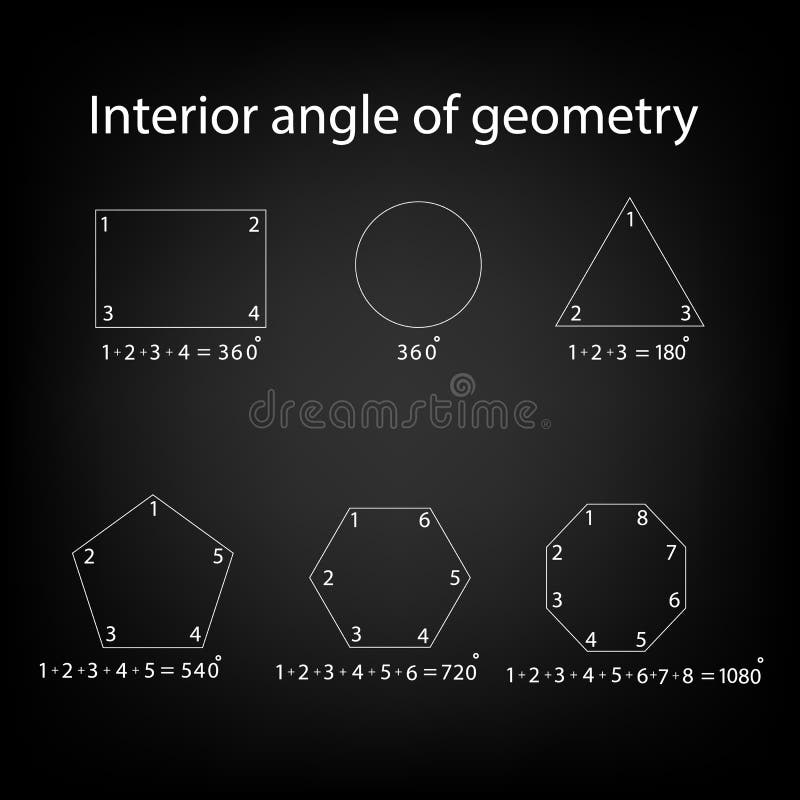



黑色背景上矩形 三角形 圆 五角形 六边形和八边形等几何的内角等式向量例证 插画包括有配方 线路




六角夹子艺术 六角形png图片素材免费下载 图片编号 Png素材网



1




魔术六角形内角 六边形png图片素材免费下载 图片编号 Png素材网




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



0 件のコメント:
コメントを投稿